Plaid CTF 2016 - Tonnerre

Public-key based authentication protocol for which we had to write a client, after finding credentials through SQL injection.

Description

We were pretty sure the service at tonnerre.pwning.xxx:8561 (source) was totally secure. But then we came across this website and now we’re having second thoughts… We think they store the service users in the same database?

Details

Points: 200

Category: crypto

Validations: 119

Solution

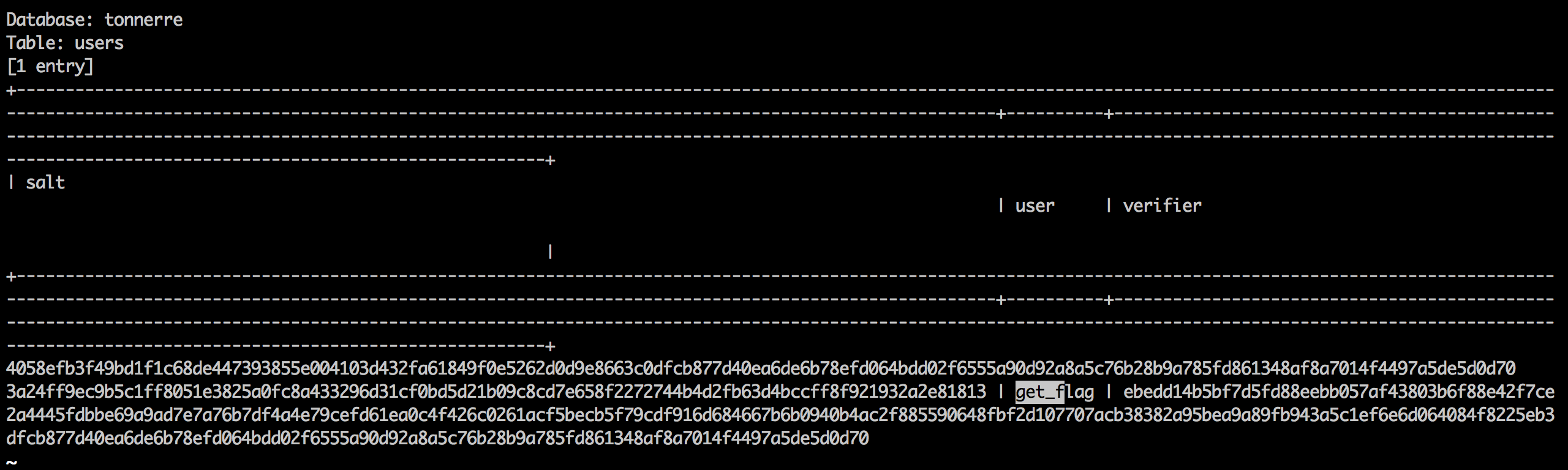
The web login form waas vulnerable to basic SQL injection. Running sqlmap directly gave the content of the table users in the database tonnerre: a single user get_flag and two values:

• salt, a random-looking 127-byte string
• verifier, a random-looking 145-byte string

These values were to be used in a public key-based authentication protocol, remotely similar to SRP, whose server side was implemented in the Python program given to us. Copying only the interesting part, with my comments:

N = ... # a 1024-bit prime number, the group modulus

g = ... # a 671-bit number, a group generator

...

   # generates a key pair
    random_server = random.randint(2, N-3)
    public_server = pow(g, random_server, N)

    # mask the public key with the verifier
    residue = (public_server + permitted_users[username][1]) % N

    # send salt and masked pubkey
    req.sendall(tostr(permitted_users[username][0]) + '\n')
    req.sendall(tostr(residue) + '\n')

    # compute the session key,
    #   masking the client pubkey with the verifier
    #   raising to the server's secret exponent
    #   hashign the whole thing using SHA-256
    session_secret = (public_client * permitted_users[username][1]) % N
    session_secret = pow(session_secret, random_server, N)
    session_key = H(tostr(session_secret))

    # receive a proof from the client..
    proof = req.recv(512).strip('\n')

    # ..should be a hash of the server's masked pubkey and session key
    if (proof != H(tostr(residue) + session_key)):
      req.sendall('Sorry, not permitted.\n')
      req.close()
      return

    # this is useless for the challenge
    our_verifier = H(tostr(public_client) + session_key)
    req.sendall(our_verifier + '\n')

    # send us the flag!
    req.sendall('Congratulations! The flag is ' + flag + '\n')
    req.close()

Let’s call (s, S) the server’s key pair and (c, C) the client’s key pair, such that g^s=S and g^c=C.

So it looks like the client receives the server’s Diffie-Hellman public key (after unmasking using the verifier), but then the shared key will be

(C * verifier)^s = g^(cs) * verifier^s

And since the client doesn’t know the server’s private exponent s we can’t determine the shared key. What’s the catch?

The trick was that public_client shouldn’t be the client’s public key C, but C multiplied by the inverse of verifier. Using the standard modular inversion algorithm, we can compute the verifier’s inverse modulo the prime N.

We could then authenticate with the following program (again, showing only the non-trivial part):

random_client = random.randint(2, N-2)
public_client = pow(g, random_client, N)

invver = modinv(verifier, N)

public_client2 = invver * public_client % N

if ((public_client2 * verifier) % N) == public_client:
    print 'verifier verified'

s.sendall(tostr(public_client2) + '\n')

# get salt and server pubkey
salt = int(s.recv(512).strip('\n'), 16) % N
residue = int(s.recv(512).strip('\n'), 16) % N
public_server = (residue - verifier + N) % N

session_secret = pow(public_server, random_client, N)
session_key = H(tostr(session_secret))

proof = H(tostr(residue) + session_key)

s.sendall(proof + '\n')
time.sleep(0.5)
r = s.recv(512).strip('\n')
print r

Then:

python tonnerre_solve.py
Welcome to the Tonnerre Authentication System!

verifier verified
ca787059bc572bc7902c91d2a168226a32052518073f4c32948ff02826e6be22
Congratulations! The flag is PCTF{SrP_v1_BeSt_sRp_c0nf1rm3d}

Written on April 18, 2016