DEFCON qualifiers 2016 - Baby-re

Remote binary asks for 13 values, looking at the binary we find out that the condition is a system of linear equations over 32-bit signed integers. We find the equations from the binary and solve them to find the unique solution.

Description

N.A.

Details

Points: variable

Category: baby’s first

Validations: a lot

Solution

We’re given the binary of a remote service:

$ file baby-re
baby-re: ELF 64-bit LSB executable, x86-64, version 1 (SYSV),
dynamically linked (uses shared libs), for GNU/Linux 2.6.32, not
stripped

This asks for 13 inputs, and then returns Wrong, unless we give it the right input.

$ ./baby-re
Var[0]: 1
Var[1]: 2
Var[2]: 3
Var[3]: 4
Var[4]: 5
Var[5]: 6
Var[6]: 7
Var[7]: 8
Var[8]: 9
Var[9]: 10
Var[10]: 11
Var[11]: 12
Var[12]: 13
Wrong

A little reverse engineering was needed to understand the condition. The binary wasn’t packed, contained symbols and functions names. The interesting function was obvious: CheckSolution:

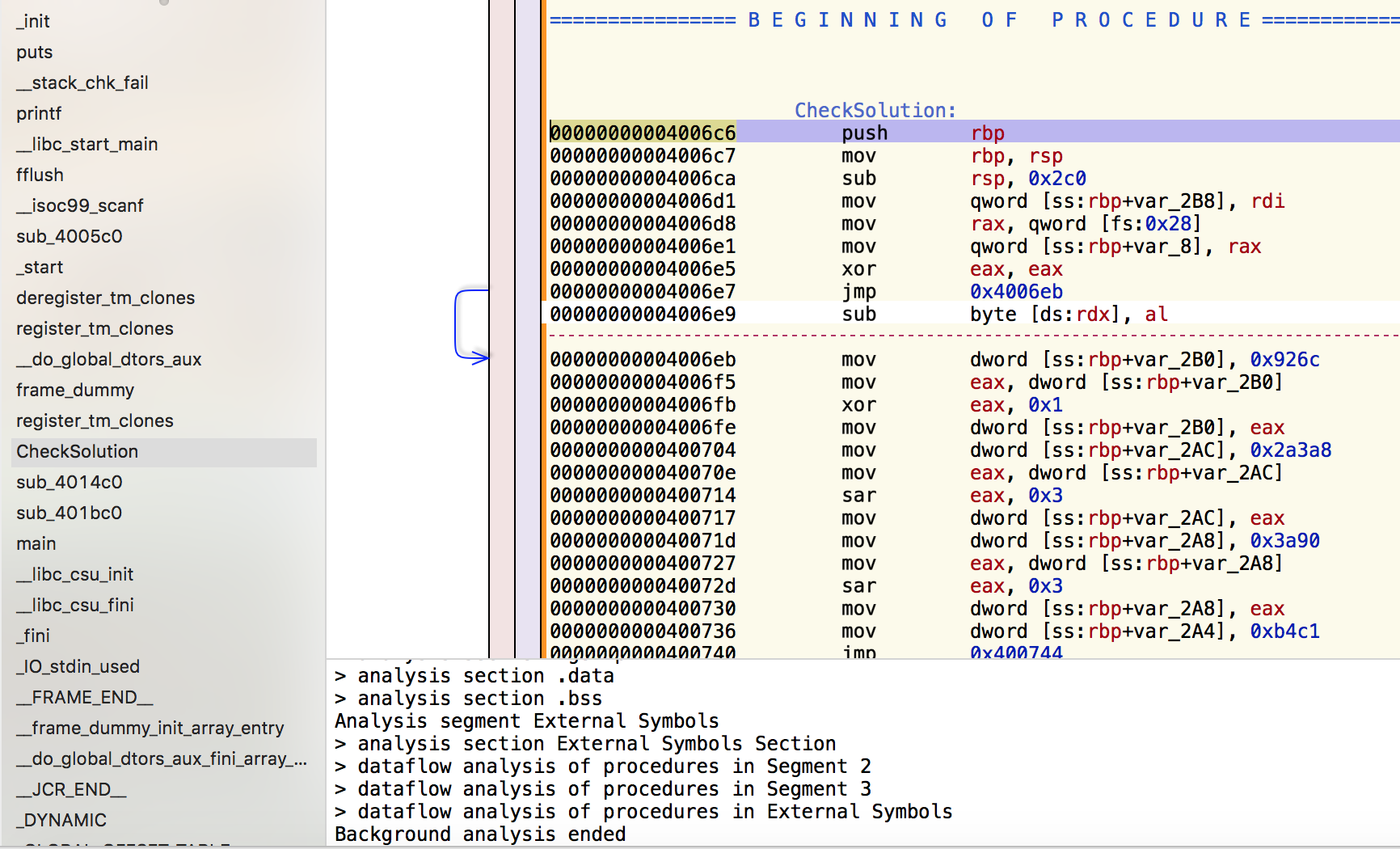
Interestingly, Hopper gave right away an (almost) correct decompiled code for CheckSolution’s, whereas Hexrays failed due to the simple anti-reverse tricks. (Even after getting rid of these protections, IDA gave us a much cleaner C code than Hopper, but that included a few errors.)

CheckSolution first computed a bunch of constants, which were then used as coefficient of a linear system of equations over signed 32-bit integers. The 13 solutions were the numbers expected by the command-line argument.

We went from the decompiled code

    if (*(int32_t *)(var_2B8 + 0x30) * 0xd5e5 + *(int32_t *)(var_2B8 + 0x2c) * 0x99ae + \
    *(int32_t *)(var_2B8 + 0x28) * var_288 + *(int32_t *)(var_2B8 + 0x24) * 0x3922 + \
    *(int32_t *)(var_2B8 + 0x20) * 0xe15d + *(int32_t *)(var_2B8 + 0x1c) * var_294 + \
    *(int32_t *)(var_2B8 + 0x18) * var_298 + *(int32_t *)(var_2B8 + 0x14) * 0xa89e + \
    (var_2B0 * *(int32_t *)var_2B8 - *(int32_t *)(var_2B8 + 0x4) * var_2AC - \
    *(int32_t *)(var_2B8 + 0x8) * var_2A8 - *(int32_t *)(var_2B8 + 0xc) * 0xb4c1) + \
    *(int32_t *)(var_2B8 + 0x10) * var_2A0 != 0x1468753) {
            rax = 0x0;
    }
    else {
            if (*(int32_t *)(var_2B8 + 0x30) * 0xcfec + (*(int32_t *)(var_2B8 + 0x14) * var_268 + \
            *(int32_t *)(var_2B8 + 0x10) * 0x39ca + (var_27C * *(int32_t *)var_2B8 + \
            *(int32_t *)(var_2B8 + 0x4) * var_278 - *(int32_t *)(var_2B8 + 0x8) * 0x1783) + \
            *(int32_t *)(var_2B8 + 0xc) * 0x9832 - *(int32_t *)(var_2B8 + 0x18) * 0x345 - \
            *(int32_t *)(var_2B8 + 0x1c) * var_260 - *(int32_t *)(var_2B8 + 0x20) * 0xc5a0 - \
            *(int32_t *)(var_2B8 + 0x24) * 0x2e35 - *(int32_t *)(var_2B8 + 0x28) * 0x4e4e - \
            *(int32_t *)(var_2B8 + 0x2c) * var_250) != 0x162f30) {
                    rax = 0x0;
            }
            else {
(...)

to equations expressed as a list of coefficients within a Numpy array (with our original commented lines):

import numpy as np

res = np.array([21399379, 1453872, -5074020, -5467933, 7787144,
-8863847, -747805, -11379056, -166140, 9010363, -4169825, 4081505,
1788229,])

eqs = np.array([
# hexrays gives 0 for v[9] -> WRONG
[ 37485, -21621, -1874, -46273, 50633, 43166, 29554, 16388, 57693, 14626, 21090, 39342, 54757,],
#[ 37485, -21621, -1874, -46273, 50633, 43166, 29554, 16388, 57693, 0, 21090, 39342, 54757,],
[ 50936, 4809, -6019, 38962, 14794, 22599, -837, -36727, -50592, -11829, -20046, -9256, 53228,],
[ -38730, 52943, -16882, 26907, -44446, -18601, -65221, -47543, 17702, -33910, 42654, 5371, 11469,],
[ 57747, -23889, -26016, -25170, 54317, -32337, 10649, 34805, -9171, -22855, 8621, -634, -11864,],
[ -14005, 16323, 43964, 34670, 54889, -6141, -35427, -61977, 28134, 43186, -59676, 15578, 50082,],
[ -40760, -22014, 13608, -4946, -26750, -31708, 39603, 13602, -59055, -32738, 29341, 10305, -15650,],
[ -47499, 57856, 13477, -10219, -5032, -21039, -29607, 55241, -6065, 16047, -4554, -2262, 18903,],
[ -65419, 17175, -9410, -22514, -52377, -9235, 53309, 47909, -59111, -41289, -24422, 41178, -23447,],
#hopper's correct
[ 1805, 4135, -16900, 33381, 46767, 58551, -34118, -44920, -11933, -20530, 15699, -36597, 18231,],
# hexrays version -> WRONG
#[ 1805, 4135, -16900, 33381, 33422, 58551, -34118, -44920, -11933, -20530, 15699, -36597, 18231,],
[ -42941, 61056, -45169, 41284, -1722, -26423, 47052, 42363, 15033, 18975, 10788, -33319, 63680,],  
[ -37085, -51590, -17798, -10127, -52388, 12746, 12587, 58786, -8269, 22613, 30753, -20853, 32216,],
# hopper got wrong sign here for some reason
#[ 36650, 47566, -33282, -59180, 65196, 9228, -59599, -62888, 48719, 47348, 37592, 57612, 40510,],
[ 36650, 47566, -33282, -59180, 65196, 9228, -59599, -62888, 48719, 47348, -37592, 57612, 40510,],
[ 51735, 35879, -63890, 4102, 59511, -21386, -20769, 26517, 28153, 25252, -43789, 25633, 7314,],
])

Then we solved the system using Numpy’s solver:

x = np.linalg.solve(eqs, res)
print(x)

which gave us the solution

[  77.   97.  116.  104.   32.  105.  115.   32.  104.   97.  114.  100.  33.]

And indeed, this gives us the flag:

$ ./baby-re
Var[0]: 77
Var[1]: 97
Var[2]: 116
Var[3]: 104
Var[4]: 32
Var[5]: 105
Var[6]: 115
Var[7]: 32
Var[8]: 104
Var[9]: 97
Var[10]: 114
Var[11]: 100
Var[12]: 33
The flag is: Math is hard!

You’ll find the source published by Legitbs, and other solutions using mathematica or angr (much simpler!).

Written on May 23, 2016